Triangular Global Alignment Kernels

Why (Triangular) Global Alignment kernels rather than Dynamic Time Warping kernels?

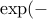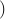Dynamic Time Warping (DTW) is widely used for retrieval, that is to find the closest match(es) in a database given a time series of interest. My intuition, illustrated in the video above, is that DTW does not quantify dissimilarity in a meaningful way, which was somehow a known fact since the DTW distance does not satisfy the triangular inequality and DTW is not positive definite.
In kernel methods, both large and small similarities matter, since they all contribute to the Gram matrix. Global Alignment (GA) kernels, which are positive definite, seem to do a better job of quantifying all similarities coherently, because they consider all possible alignments.
Triangular Global Alignment (TGA) kernels consider a smaller subset of such alignments. They are faster to compute and positive definite, and can be seen as trade-off between the full GA kernel (accurate, versatile but slow) and a Gaussian kernel (fast but limited) as discussed below.

Implementations

Matlab Mex implementation of GA kernels: logGAK.c.

To compile and use directly from Matlab, type mex logGAK.c from the Matlab prompt to get a mex executable such as logGAK.mexmaci64 if you are running a Mac, logGAK.mexglx on linux or logGAK.mexw32 on windows. NOTE: you have to uncomment lines 62–66 if you want to compile logGAK.c with mex on windows platforms. Do not change anything if you are compiling it with Mac/Linux.

Python wrapper TGA_python_wrapper, courtesy of Adrien Gaidon

In practice

logGAK compares two time-series using the Kernel bandwidth and Triangular parameters:
- When Triangular is set to , the routine returns the original GA kernel, that is
  $k(mathbf{x},mathbf{y})=sum_{piinmathcal{A}(n,m)}prod_{i=1}^{|pi|}kappa(x_{pi_1(i)},y_{pi_2(i)}),$
  where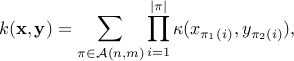 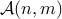is the set of all possible alignments between two series of length 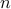and 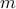. In this new implementation we do not use the Gaussian kernel for and consider instead
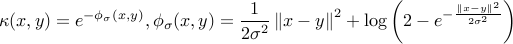
  $kappa(x,y)= e^{-phi_sigma(x,y)}, phi_sigma(x,y)=frac{1}{2sigma^2}left|x-yright|^2+logleft(2-e^{-frac{left|x-yright|^2}{2sigma^2}}right)$
- When Triangular is bigger than 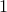the routine only considers alignments for which 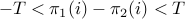for all indices of the alignment. When this parameter is set to 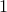, the kernel becomes the kernel
  $k_{T=1}(mathbf{x},mathbf{y})= delta(|mathbf{x}|=|mathbf{y}|)prod_{i=1}^{|mathbf{x}|} e^{-phi_sigma(x_i,y_i)}$
  between time series, which is non-zero for series of the same length only. It is a slightly modified Gaussian kernel between vectors which does not take into account the temporal structure of time series. When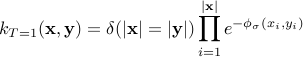 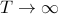, the Triangular kernel's values converge to that of the usual GA kernel. The smaller 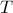the shorter the runtime for each iteration of logGAK.

Parameter tuning advice:
- The Bandwidth 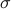can be set as a multiple of a simple estimate of the median distance of different points observed in different time-series of your training set, scaled by the square root of the median length of time-series in the training set. This is because the scale of
  $k(mathbf{x},mathbf{y})= prod_{i=1}^{|pi|}e^{-phi_{sigma}(x_{pi_1(i)},x_{pi_2(i)})}$
  is infuenced by the length of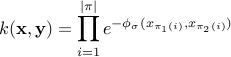 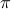, which is of the order of the median length, and also by the values taken by 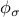, which are of the order of median distances between points. You can try
  
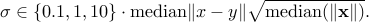
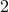  I have observed in experiments that higher multiples (e.g or 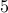) seem to work better.
- The Triangular parameter 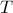can be set to a reasonable multiple of the median length, e.g 0.2 or 0.5. Note that whenever two time-series’ length differ by more than 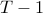, their kernel value is equal to .

Example: generate two random multivariate (dimension 5) time-series of length 12 and 8, compute their log-kernel and their normalized kernel by taking into account the diagonal terms logGAK(X,X,2,0) and logGAK(Y,Y,2,0).

>> rand('state',0); X=rand(12,5); Y=rand(8,5); logGAK(X,Y,2,0)

ans =

10.4026

>> exp(logGAK(X,Y,2,0)-.5*(logGAK(X,X,2,0)+logGAK(Y,Y,2,0)))

ans =

0.1592

Global Alignment Kernels (deprecated)

function coded in c++ that takes two sequences of vectors as inputs, that is two matrices n1 x d and n2 x d, and computes the corresponding (log)kernel value. If your sequence is not made of vectors, you can easily input directly the Gram matrix grammat instead.
Matlab function DTWKMatlab.m that does the same thing,
better and faster, the DTWK.c mex sourcefile.